Initialization

Before we actually begin the simulation, we first initialize all of the various data structures that will be used. A simulation file containing the geometric and dynamic properties of the various objects in the simulation are read into Impulse. This file also contains the initial poses and wrenches to apply to each object in the simulation.

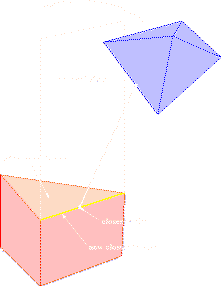
Objects are read in and distributed across the processors. This is done using a spread array structure provided by Split-C. The advantage is that each processor is in charge of maintaining the state of a smaller subset of the objects thereby exploiting the parallelism during various stages of the simulation. Fixed objects are local to all processors as well as static data about all of the objects such as their polygonal models, tiling resolution, etc. The result is that objects in collision with fixed objects or with objects that are local to the same processor achieve near linear parallel speedup results.

---

Next the closest feature table is initialized. This table is used by the Lin-Canny algorithm to find the next closest feature pair between two objects. This simply provides a starting pair for the algorithm. This table can be quite large for many objects with large numbers of facets. Below is a depiction of a closest feature pair between two objects.

Since this portion of the initialization step is only done once at the beginning of the simulation no parallelization was made for the computing the initial closest features. Instead this is performed entirely on one processor. This is not a problem since we only perform this initialization once. The closest feature table is a global structure visible to all processors. The disadvantage is that it resides on one processor, hence often lookups into the table will require one integer of data to be transmitted between processors. Future improvements to this could be easily be made if time permitted.

---

We then compute initial bounding volumes of the objects and place them into a data structure for the

Here we exploit some of the parallelism such that all of the processors compute the bounding volumes of their local objects and place them into the global hash tiling. The bounding volume calculations all occur in parallel for the objects. Access to the hash tiling structure is made via atomic access routines to the hash bins. Objects that don't hash to the same spatial hash tiling will not be in contention for the same block of data and hence will proceed to operate in parallel. Future improvements involving distributing the hash across processors could be made to this routine. However, given the size of the project many of these such optimizations were not made in the sake of getting a fully and correctly operating simulation running within the time frame given by this project.

---

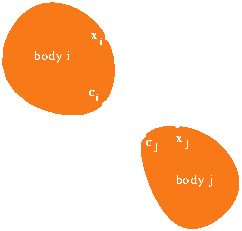Finally, we initialize the collision heap. This data structure is heap ordered by the estimated time to impact of each object pair. As explained in the previous section, we need only keep objects that are close to one another in the heap. For "close" object pairs we can estimate the soonest time to collision by examining the acceleration and velocity components of the two objects along the vector representing the closest distance between them. We also take the angular components into account along with an energy conservation argument. The result is a time estimate of the soonest time to impact for the object pair. We are guaranteed that no collision can occur between this pair any sooner than this time bound.

Again since this portion of the initialization step is only performed once at the beginning of the simulation no parallelization was made for computing the initial time to impact between object pairs. Instead this portion of the code is performed entirely on one processor. This is not a problem since we only perform this initialization once. The collision heap resides on only one processor. This is not a problem for the parallel implementation as discussion in the next step of the operation. An earlier approach to this problem on a 2D system also explored the results of randomly spreading the heap across processors.