The hash tiling we used is a technique developed by Mark Overmars at the Computer Science Department at the University of Utrecht. He describes the technique in the paper "Point Location in Fat Subdivisions" where he gives an algorithm for computing the intersection of n such bounding volume boxes in O(n(1+log R)) time, where R is the ration of the smallest to largest box size.

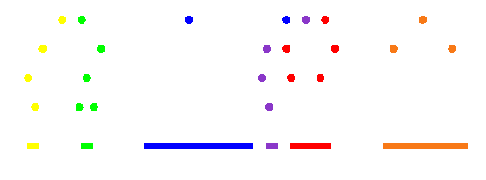
In the one dimensional example above each object has a pre-computed hash resolution size that remains constant throughout the simulation. Objects are placed into the tiling at their pre-computed resolution and all such larger resolutions (numbered as smaller numbers in the figure above). When a intersection check is made, we simply take the smallest shared resolution of the two objects (numbered as larger numbers on the figure above) and hash to that location. In the bin returned by that hash lookup we will be able to observe if the two objects share a volume. In addition we will be able to determine all such objects that intersect the object's swept volume. In the example above only the objects with arrows drawn between them at the bottom would be considered as having intersecting hash tilings.
When we insert an object's hashed volume into the tiling we can immediately determine the other neighboring objects' volumes that intersect with this new hash volume. From that we can decide if any new objects should be placed into the collision heap. The major advantage of this tiling is to keep the heap small which significantly reduces the update time after a collision.
| After parallel computation of the swept volumes for all of the objects in the simulation, we determine the new hash entries that need to be inserted into the spatial hash tiling. If an object's bounding volume has not changed since it was last updated, no work is required and no modifications to the hash tiling are made for that object. When new hash entries need to be inserted and old ones removed we use atomic operations for accessing each bin. Access to the tiling data structure can be performed in parallel when processors are making updates to different spatial hash tiling bins. Although when objects are clustered together they will hash into the same spatial hash tiling bin, remember that we only require atomic access to the bin for updates and that we only make updates when an object enters or exits a bin. Therefore, objects that remain close to one another, hence share a spatial hash tiling bin, will not receive any performance hit after their initial insertion into the bin since there will be no futher contention for atomic access to the tiling as expected. |
